小林 正典*, 青木 宏之*, 祖田 直也*, （* 茨城大学）
Zero Fields and Geometrical Properties of Singular Equipotential Lines
Masanori Kobayashi*, Hiroyuki Aoki*, Naoya Soda*, (* Ibaraki University)
Magnetic(or electric) fields produced by the point charges have the points of equilibrium on which the magnitudes of magnetic(or electric) field vectors are zero. Those points are called the singular points. Those points give the zero magnetic(or electric) fields in the Phi science. The magnetic field produced by the point charges has the unique relation with the electric field produced by the point charges. Therefore, the present paper considers the electric fields produced by the point charges placed on the plane. These electric fields have n+1 singular points of n saddle points and one point at the center. The equipotential lines passing through those all saddle points are called the singular equipotential lines in the present paper. The figures of the singular equipotential lines are of equilibrium and beautiful. The geometrical properties of the singular equipotential lines are clarified by letting those be treated as one figure and be related to the knots and the links of the knot theory in mathematics: the knots (2m+1)1 for the cases of odd number-point charges and the links (2m)
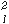for the cases of even number-point charges.
Keywords : zero magnetic fields, point of equilibrium, singular point, singular equipotential lines, knot, link
Received : July, 15, 2011
Accepted : August, 5, 2011